Introduction to Graphs
Real-world graphs
Graph-structured data have been widely utilized in many real-world scenarios. For example, each user on Facebook can be seen as a vertex and their relations like friendship or followership can be seen as edges in the graph. We might be interested in predicting the interests of users, or whether a pair of nodes in a network might have an edge connecting them.
A graph can be represented using an adjacency matrix
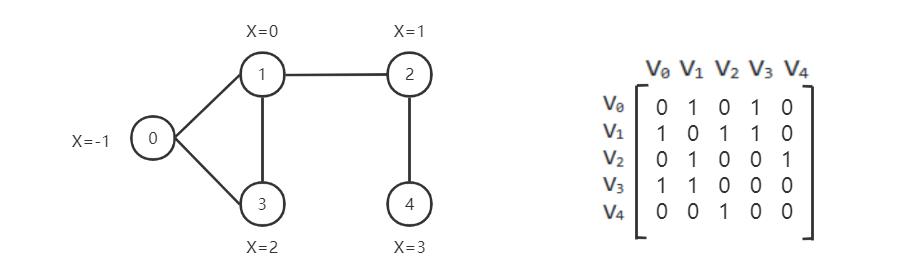
How to represent a graph in CogDL
A graph is used to store information of structured data. CogDL represents a graph with a cogdl.data.Graph object.
Briefly, a Graph holds the following attributes:
x: Node feature matrix with shape[num_nodes, num_features], torch.Tensoredge_index: COO format sparse matrix, Tupleedge_weight: Edge weight with shape[num_edges,], torch.Tensoredge_attr: Edge attribute matrix with shape[num_edges, num_attr]y: Target labels of each node, with shape[num_nodes,]for single label case and [num_nodes, num_labels] for mult-label caserow_indptr: Row index pointer for CSR sparse matrix, torch.Tensor.col_indices: Column indices for CSR sparse matrix, torch.Tensor.num_nodes: The number of nodes in graph.num_edges: The number of edges in graph.
The above are the basic attributes but are not necessary. You may define a graph with g = Graph(edge_index=edges) and omit the others.
Besides, Graph is not restricted to these attributes and other self-defined attributes, e.g., graph.mask = mask, are also supported.
Represent this graph in cogdl:
|
|
Graph stores sparse matrix with COO or CSR format. COO format is easier to add or remove edges, e.x. add_self_loops, and CSR is stored for fast message-passing.
Graph automatically convert between two formats and you can use both on demands without worrying. You can create a Graph with edges or assign edges
to a created graph. edge_weight will be automatically initialized as all ones, and you can modify it to fit your need.
import torch
from cogdl.data import Graph
edges = torch.tensor([[0,1],[1,3],[2,1],[4,2],[0,3]]).t()
x = torch.tensor([[-1],[0],[1],[2],[3]])
g = Graph(edge_index=edges,x=x) # equivalent to that above
print(g.row_indptr)
>>tensor([0, 2, 3, 4, 4, 5])
print(g.col_indices)
>>tensor([1, 3, 3, 1, 2])
print(g.edge_weight)
>> tensor([1., 1., 1., 1., 1.])
g.num_nodes
>> 5
g.num_edges
>> 5
g.edge_weight = torch.rand(5)
print(g.edge_weight)
>> tensor([0.8399, 0.6341, 0.3028, 0.0602, 0.7190])
We also implement commonly used operations in Graph:
add_self_loops: add self loops for nodes in graph,
add_remaining_self_loops: add self-loops for nodes without it.sym_norm: symmetric normalization of edge_weight used GCN:
row_norm: row-wise normalization of edge_weight:
degrees: get degrees for each node. For directed graph, this function returns in-degrees of each node.
import torch
from cogdl.data import Graph
edge_index = torch.tensor([[0,1],[1,3],[2,1],[4,2],[0,3]]).t()
g = Graph(edge_index=edge_index)
>> Graph(edge_index=[2, 5])
g.add_remaining_self_loops()
>> Graph(edge_index=[2, 10], edge_weight=[10])
>> print(edge_weight) # tensor([1., 1., ..., 1.])
g.row_norm()
>> print(edge_weight) # tensor([0.3333, ..., 0.50])
subgraph: get a subgraph containing given nodes and edges between them.edge_subgraph: get a subgraph containing given edges and corresponding nodes.sample_adj: sample a fixed number of neighbors for each given node.
from cogdl.datasets import build_dataset_from_name
g = build_dataset_from_name("cora")[0]
g.num_nodes
>> 2708
g.num_edges
>> 10556
# Get a subgraph contaning nodes [0, .., 99]
sub_g = g.subgraph(torch.arange(100))
>> Graph(x=[100, 1433], edge_index=[2, 18], y=[100])
# Sample 3 neighbors for each nodes in [0, .., 99]
nodes, adj_g = g.sample_adj(torch.arange(100), size=3)
>> Graph(edge_index=[2, 300]) # adj_g
train/eval: In inductive settings, some nodes and edges are unseen during training,train/evalprovides access to switching backend graph for training/evaluation. In transductive setting, you may ignore this.
# train_step
model.train()
graph.train()
# inference_step
model.eval()
graph.eval()
How to construct mini-batch graphs
In node classification, all operations are in one single graph. But in tasks like graph classification, we need to deal with
many graphs with mini-batch. Datasets for graph classification contains graphs which can be accessed with index, e.x. data[2].
To support mini-batch training/inference, CogDL combines graphs in a batch into one whole graph, where adjacency matrices form sparse block diagnal matrices
and others(node features, labels) are concatenated in node dimension. cogdl.data.Dataloader handles the process.
from cogdl.data import DataLoader
from cogdl.datasets import build_dataset_from_name
dataset = build_dataset_from_name("mutag")
>> MUTAGDataset(188)
dataset[0]
>> Graph(x=[17, 7], y=[1], edge_index=[2, 38])
loader = DataLoader(dataset, batch_size=8)
for batch in loader:
model(batch)
>> Batch(x=[154, 7], y=[8], batch=[154], edge_index=[2, 338])
batch is an additional attributes that indicate the respective graph the node belongs to. It is mainly used to do global
pooling, or called readout to generate graph-level representation. Concretely, batch is a tensor like:
The following code snippet shows how to do global pooling to sum over features of nodes in each graph:
def batch_sum_pooling(x, batch):
batch_size = int(torch.max(batch.cpu())) + 1
res = torch.zeros(batch_size, x.size(1)).to(x.device)
out = res.scatter_add_(
dim=0,
index=batch.unsqueeze(-1).expand_as(x),
src=x
)
return out
How to edit the graph?
Changes can be applied to edges in some settings. In such cases, we need to generate a graph for calculation while keep the original graph. CogDL provides graph.local_graph to set up a local scape and any out-of-place operation will not reflect to the original graph. However, in-place operation will affect the original graph.
graph = build_dataset_from_name("cora")[0]
graph.num_edges
>> 10556
with graph.local_graph():
mask = torch.arange(100)
row, col = graph.edge_index
graph.edge_index = (row[mask], col[mask])
graph.num_edges
>> 100
graph.num_edges
>> 10556
graph.edge_weight
>> tensor([1.,...,1.])
with graph.local_graph():
graph.edge_weight += 1
graph.edge_weight
>> tensor([2.,...,2.])
Common graph datasets
CogDL provides a bunch of commonly used datasets for graph tasks like node classification, graph classification and others. You can access them conveniently shown as follows.
from cogdl.datasets import build_dataset_from_name
dataset = build_dataset_from_name("cora")
from cogdl.datasets import build_dataset
dataset = build_dataset(args) # if args.dataet = "cora"
For all datasets for node classification, we use train_mask, val_mask, test_mask to denote train/validation/test split for nodes.
CogDL now supports the following datasets for different tasks:
Network Embedding (Unsupervised node classification): PPI, Blogcatalog, Wikipedia, Youtube, DBLP, Flickr
Semi/Un-superviesd Node classification: Cora, Citeseer, Pubmed, Reddit, PPI, PPI-large, Yelp, Flickr, Amazon
Heterogeneous node classification: DBLP, ACM, IMDB
Link prediction: PPI, Wikipedia, Blogcatalog
Multiplex link prediction: Amazon, YouTube, Twitter
graph classification: MUTAG, IMDB-B, IMDB-M, PROTEINS, COLLAB, NCI, NCI109, Reddit-BINARY
Network Embedding(Unsupervised Node classification)
Dataset |
Nodes |
Edges |
Classes |
Degree |
Name in Cogdl |
|---|---|---|---|---|---|
PPI |
3,890 |
76,584 |
50(m) |
— |
ppi-ne |
BlogCatalog |
10,312 |
333,983 |
40(m) |
32 |
blogcatalog |
Wikipedia |
4.777 |
184,812 |
39(m) |
39 |
wikipedia |
Flickr |
80,513 |
5,899,882 |
195(m) |
73 |
flickr-ne |
DBLP |
51,264 |
2,990,443 |
60(m) |
2 |
dblp-ne |
Youtube |
1,138,499 |
2,990,443 |
47(m) |
3 |
youtube-ne |
Node classification
Dataset |
Nodes |
Edges |
Features |
Classes |
Train/Val/Test |
Degree |
Name in cogdl |
|---|---|---|---|---|---|---|---|
Cora |
2,708 |
5,429 |
1,433 |
7(s) |
140 / 500 / 1000 |
2 |
cora |
Citeseer |
3,327 |
4,732 |
3,703 |
6(s) |
120 / 500 / 1000 |
1 |
citeseer |
PubMed |
19,717 |
44,338 |
500 |
3(s) |
60 / 500 / 1999 |
2 |
pubmed |
Chameleon |
2,277 |
36,101 |
2,325 |
5 |
0.48 / 0.32 / 0.20 |
16 |
chameleon |
Cornell |
183 |
298 |
1,703 |
5 |
0.48 / 0.32 / 0.20 |
1.6 |
cornell |
Film |
7,600 |
30,019 |
932 |
5 |
0.48 / 0.32 / 0.20 |
4 |
film |
Squirrel |
5201 |
217,073 |
2,089 |
5 |
0.48 / 0.32 / 0.20 |
41.7 |
squirrel |
Texas |
182 |
325 |
1,703 |
5 |
0.48 / 0.32 / 0.20 |
1.8 |
texas |
Wisconsin |
251 |
515 |
1,703 |
5 |
0.48 / 0.32 / 0.20 |
2 |
Wisconsin |
PPI |
14,755 |
225,270 |
50 |
121(m) |
0.66 / 0.12 / 0.22 |
15 |
ppi |
PPI-large |
56,944 |
818,736 |
50 |
121(m) |
0.79 / 0.11 / 0.10 |
14 |
ppi-large |
232,965 |
11,606,919 |
602 |
41(s) |
0.66 / 0.10 / 0.24 |
50 |
||
Flickr |
89,250 |
899,756 |
500 |
7(s) |
0.50 / 0.25 / 0.25 |
10 |
flickr |
Yelp |
716,847 |
6,977,410 |
300 |
100(m) |
0.75 / 0.10 / 0.15 |
10 |
yelp |
Amazon-SAINT |
1,598,960 |
132,169,734 |
200 |
107(m) |
0.85 / 0.05 / 0.10 |
83 |
amazon-s |
Heterogenous Graph
Dataset |
Nodes |
Edges |
Features |
Classes |
Train/Val/Test |
Degree |
Edge Type |
Name in Cogdl |
|---|---|---|---|---|---|---|---|---|
DBLP |
18,405 |
67,946 |
334 |
4 |
800 / 400 / 2857 |
4 |
4 |
gtn-dblp(han-acm) |
ACM |
8,994 |
25,922 |
1,902 |
3 |
600 / 300 / 2125 |
3 |
4 |
gtn-acm(han-acm) |
IMDB |
12,772 |
37,288 |
1,256 |
3 |
300 / 300 / 2339 |
3 |
4 |
gtn-imdb(han-imdb) |
Amazon-GATNE |
10,166 |
148,863 |
— |
— |
— |
15 |
2 |
amazon |
Youtube-GATNE |
2,000 |
1,310,617 |
— |
— |
— |
655 |
5 |
youtube |
10,000 |
331,899 |
— |
— |
— |
33 |
4 |
Knowledge Graph Link Prediction
Dataset |
Nodes |
Edges |
Train/Val/Test |
Relations Types |
Degree |
Name in Cogdl |
|---|---|---|---|---|---|---|
FB13 |
75,043 |
345,872 |
316,232 / 5,908 / 23,733 |
12 |
5 |
fb13 |
FB15k |
14,951 |
592,213 |
483,142 / 50,000 / 59,071 |
1345 |
40 |
fb15k |
FB15k-237 |
14,541 |
310,116 |
272,115 / 17,535 / 20,466 |
237 |
21 |
fb15k237 |
WN18 |
40,943 |
151,442 |
141,442 / 5,000 / 5,000 |
18 |
4 |
wn18 |
WN18RR |
86,835 |
93,003 |
86,835 / 3,034 / 3,134 |
11 |
1 |
wn18rr |
Graph Classification
TUdataset from https://www.chrsmrrs.com/graphkerneldatasets
Dataset |
Graphs |
Classes |
Avg. Size |
Name in Cogdl |
|---|---|---|---|---|
MUTAG |
188 |
2 |
17.9 |
mutag |
IMDB-B |
1,000 |
2 |
19.8 |
imdb-b |
IMDB-M |
1,500 |
3 |
13 |
imdb-m |
PROTEINS |
1,113 |
2 |
39.1 |
proteins |
COLLAB |
5,000 |
5 |
508.5 |
collab |
NCI1 |
4,110 |
2 |
29.8 |
nci1 |
NCI109 |
4,127 |
2 |
39.7 |
nci109 |
PTC-MR |
344 |
2 |
14.3 |
ptc-mr |
REDDIT-BINARY |
2,000 |
2 |
429.7 |
reddit-b |
REDDIT-MULTI-5k |
4,999 |
5 |
508.5 |
reddit-multi-5k |
REDDIT-MULTI-12k |
11,929 |
11 |
391.5 |
reddit-multi-12k |
BBBP |
2,039 |
2 |
24 |
bbbp |
BACE |
1,513 |
2 |
34.1 |
bace |

